Limits of Polynomial and Rational Functions
Lesson 12.2 discusses several processes by which limits may be evaluated:
Direct Substitution
Direct Substitution is a viable approach only when a function is continuous. For example, the function below is continuous, and by using direct substitution, the limit is revealed:
Substitute 6 for x, and 0 results. Therefore, the limit is 0.
Definition of a Continuous:
However, not all limits can be evaluated by direct substitution, as stated above. Another approach must be taken to evalute these limits. The first of these techniques is found below:
Dividing Out
Direct substitution is not an option for the function below as it is not continutous:
If direct substitution is used both the numerator and denominator will be zero. However, unlike in previous lessons, this does not mean that the limit is undefined. It means that the limit is Indeterminate, that is, a limit may or may not exist. Another method must be employed to find out.
Dividing out involves the canceling out of common terms in a function. Factoring is one method that may be used to accomplish this. When the above limit is factored, the following results, and (x - 1) may be canceled out. In addition, another way to view the discontinuity of the function is by noticing that a hole exists where x = 1:
Once (x - 1) has been canceled out, direct substitution may be employed:
7 is revealed to be the limit.
Also, in cases where factoring is not an option, other techniques can be used in the dividing out method. For example, synthetic division can be used to evaluate the function below:In addition to the dividing out method, another method exists for evaluating limits of discontinuous functions:
RationalizingSimplify and cross out like terms:
As with the dividing out method, direct substitution can now be employed to evaluate the limit:
The limit is one-half.










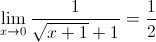
No comments:
Post a Comment