Section 5.5 (part 1, pages 411-413): Double-Angle Formulas
SINE 
COSINE 
TANGENT 
*These formulas are the most commonly used multiple-angle formulas. Like other trigonometric identities, they are used to rewrite trigonometric functions in more convenient forms.
Proof of the SINE formula: 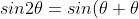)
Proof of the COSINE formula: 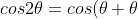)
Proof of the TANGENT formula: 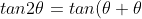)
*Compared to others, the proofs for the double-angle formulas are simple. Their basis are the Sum & Difference Formulas for sine, cosine, and tangent (Section 5.4, page 404).
Practice Problem (page 411): Solving a Double-Angle Equation
Find all solutions of 2cosx + sin2x = 0
1. 2cosx + 2sinxcosx = 0 (substitute the SINE double-angle formula for sin2x)
2. 2cosx(1 + sinx) = 0 (factor out a 2cosx)
3. 2cosx = 0, 1 + sinx = 0 (set both factors equal to 0)
4. cosx = 0, sin = -1 (simplify both factors)
6. x =  (eliminate duplicate solutions)
(eliminate duplicate solutions)
*Depending on the period of the equation, there may be additional answers.
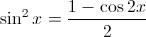







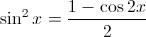







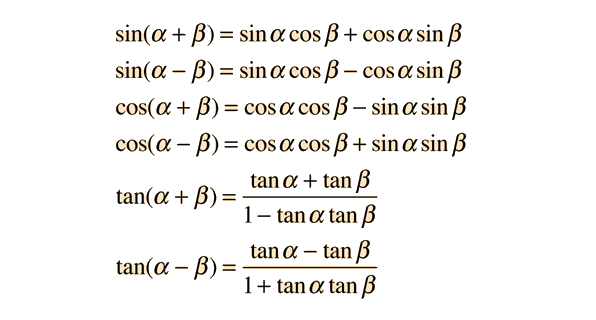









 Factoring Trigonometric Equation
Factoring Trigonometric Equation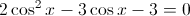







 Functions of Multiple Angles
Functions of Multiple Angles


 2.
2.



